自己动手用python写了一个线性回归。线性回归又叫最小二乘法(ordinary least squares,OLS),是回归问题当中最经典的线性方法。通过寻找参数,使得对训练集的预测值和真实值之间的均方误差最小。
线性回归是监督学习的一种,是寻找数据特征X和数据标注y之间的线性关系的方法。写线性回归首先是从一元线性回归开始写。
单变量线性回归
首先给出一组数据(x,y)寻找一种对应关系。例如下图这组数据,大致符合一种线性关系。通过线性回归就能找到相应的回归函数去最大程度的拟合这组数据。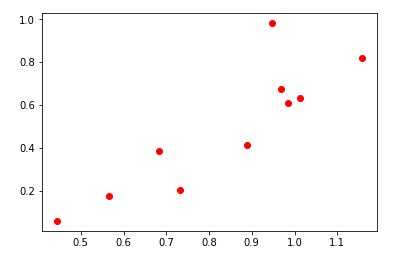
模型
模型指的是在构建整个算法时,使用的一种表达方法。我们把他称为假设函数(hypothesis)。这是一种监督学习方法的工作方式,示意图如下: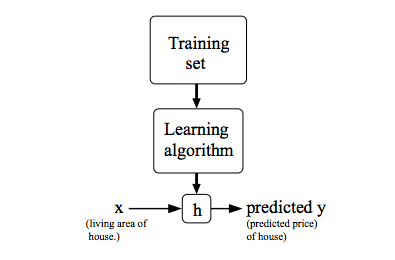
在单变量线性回归问题中,因为只含有一个输入特征。所以将模型表达为以下公式
其中是我们需要学习的参数,x是输入数据,y是目标数据。
代价函数
我们的目的是为模型寻找最适合的参数。参数的选择决定了我们所得到的模型的准确程度,通过使用代价函数来评判我们的模型准确程度。下图中模型预测值和实际值之间的差值即为建模误差(modeling error)。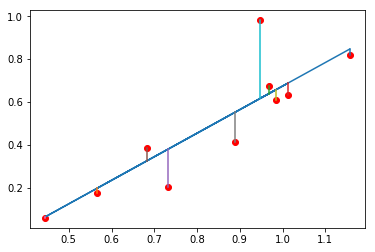
We can measure the accuracy of our hypothesis function by using a cost function. This takes an average difference (actually a fancier version of an average) of all the results of the hypothesis with inputs from x′s and the actual output y′s.
为了使得目标最小,即所得代价函数最小。
tips:为什么是除以,因为这里无论除以还是,代价函数最优化的结果都是相同的,便于计算。
梯度下降
为了使得代价函数自动降低到最小,需要通过使用一种名为梯度下降的方法。它能够自动寻找出使得代价函数最小的值。
梯度下降的原理是:开始时刻随机选择一个参数组合,计算初试代价函数,然后寻找下一个能让代价函数下降最快的参数组合。反复进行上述步骤直到得到一个局部最小值。选择不同初试参数可以得到不同局部最小值。
对赋值,使得按照梯度下降最快的方向迭代下去,其中是学习率,它决定了代价函数下降的方向步伐大小。
学习率的太大梯度下降可能会无法收敛,而学习率太小会学习速度十分低。
多元线性回归
在多元线性回归中,从单个值变成了向量,而训练值从一维向量转为矩阵。由此,假设函数也变为了矩阵形式。
同时,梯度下降中的参数也转换为向量形式,公式同上。
代码实现
一元线性回归
1 | # 模型(假设函数) |
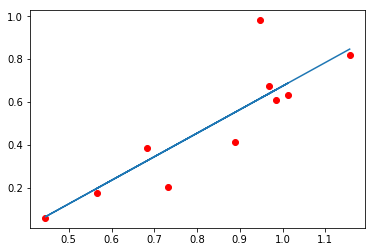
多元线性回归
1 | # 模型(假设函数) |
关于sklearn的线性回归
那sklearn.linear_model.LinearRegression中,求解线性回归方程参数时,首先判断训练集X是不是稀疏矩阵,如是,就用Golub & Kahan双对角线化过程方法来求解;否则就调用C库LAPACK中的用基于分治法的奇异值分解来求解。
以上解法和梯度下降并没有什么关系,所以说理论和实际往往还是相差很多啊。
总结
写完了用梯度下降解线性回归,作为机器学习的入门方法,在和做课后作业的时的感觉不同。这次是详细的做完了每一个步骤,也查了好多博客。后面继续努力吧。