手写ID3决策树

发表于 | 更新于

因为算法课要讲论文，就选择了Xgboost的论文，开始研究了一下决策树

什么是决策树

决策树（Decision Tree）是一种基本的分类与回归方法（ID3、C4.5和基于 Gini 的 CART 可用于分类，CART还可用于回归）。决策树在分类过程中,表示的是基于特征对实例进行划分，将其归到不同的类别。决策树的主要优点是模型可读、易于理解、分类速度快、建模与预测速度快。

构建决策树

决策树模型

决策树是由树节点与边组成的，其节点有两种类型，内部节点和叶节点，内部节点表示一个特征或者属性，叶节点代表类别。整棵树满足一个重要性质：每一个训练数据实例都被一条唯一的路径覆盖。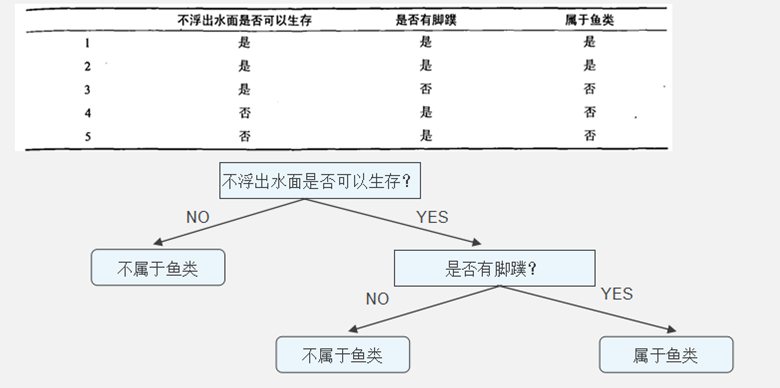

对决策树模型有了初步认识之后，接下来将介绍决策树的建模与剪枝过程，这里重点介绍 ID3 与 C4.5 ，这两种形式的决策树学习均包括三个步骤：1）特征选择；2）决策树的生成；3）减枝。接下来的段落围绕这三部分展开。

特征选择

特征选择在于选取具有分类能力的特征，来提高决策树的学习效率，通常选择特征的标准为信息增益（ID3）与信息增益比（C4.5）。首先在这里引入一个熵（Entrop）的概念。熵是表示随机变量不确定性的度量,根据熵的定义,得到随机变量的熵为：

除此之外，条件熵指的是在已知随机变量条件下随机变量的不确定性，定义如下：

通过以上定义，构造信息增益。信息增益表示的是得知特征的取值情况下使得的不确定性的减少程度。

信息增益算法如下：

至于 C4.5 完全与 ID3 类似，只不过不是采用 IG 了，而是利用信息增益比：因为用 IG 作为寻找最优划分特征时，倾向于选择特征取值多的特征，所以使用信息增益比可以校正该问题

决策树生成

经过特征选择后，接下来将进入决策树的生成算法.首先看 ID3 ，算法是这样一个过程：从根节点开始，计算特征集合的信息增益，选择增益最大的特征作为节点的特征，又该特征的不同取值构建不同的子节点，对子节点递归调用特征选择过程，直到信息增益很小或没有特征可以选择为止

生成算法这里省略掉，详情见参考文章。

决策树剪枝

决策树递归的生成，直到不能继续为止，这样产生的树往往对于训练数据十分准确，但不能很好的泛化到测试数据上，因为决策树考虑对训练数据尽可能的正确分类，从而构建出过度复杂的决策树，产生过拟合的现象，可以通过剪枝来降低树的复杂度，剪枝即裁剪掉树中的一些代表类别的叶节点，并将其数据合并到父节点作为新的叶节点，从而简化分类模型。

剪枝算法只考虑剪枝前后损失函数的差，所以剪枝可以理解为一种动态规划算法。ID3 与 C4.5 均采用这种算法即可。

代码实现

代码使用一个打网球的样例来加快理解决策树。假设今天是否去打网球（play）主要由天气（outlook）、温度（temperature）、湿度（humidity）、是否有风（windy）来确定。

假设有14条数据如下：

NO. Outlook temperature humidity windy play
1 sunny hot high FALSE no
2 sunny hot high TRUE no
3 overcast hot high FALSE yes
4 rainy mild high FALSE yes
5 rainy cool normal FALSE yes
6 rainy cool normal TRUE no
7 overcast cool normal TRUE yes
8 sunny mild high FALSE no
9 sunny cool normal FALSE yes
10 rainy mild normal FALSE yes
11 sunny mild normal TRUE yes
12 overcast mild high TRUE yes
13 overcast hot normal FALSE yes
14 rainy mild high TRUE no

计算过程

STEP1.首先计算数据集D的经验熵。
H(D)=H(play)=-((9/14)log(9/14)+(5/14)log(5/14))= 0.651756561173

STEP2.遍历所有特征，对于第i个特征A：
计算特征A对数据集D的经验条件熵H(D|A)
计算特征A的信息增益g(D,A)=H(D)-H(D|A)
选择信息增益最大的特征作为当前分裂特征。
计算outlook特征的信息增益如下：
特征A（天气）有三个不同的取值{sunny、overcast、rainy}，即v=3，根据特征A（天气）的取值，将数据集D划分为三个子集：
sunny的子集中有5个样本，2个打球（play=yes），3个不打球（play=no）；

Overcast的子集中有4个样本，都为打球（play=yes）

Rainy的子集中有5个样本，3个打球（play=yes），2个不打球（play=no）。

具体计算公式如下：
H(D|A)=H(play|outlook)=(5/14)sunny熵 + (4/14)overcast熵+ (5/14)rainy熵=(5/14)(-(2/5)log(2/5)-(3/5)log(3/5)) + (4/14)(-(4/4)log(4/4)) + (5/14)(-(3/5)log(3/5)-(2/5)*log(2/5))= 0.480722619292

所以天气特征的信息增益为：g(D,A)=g(D,outlook)=H(D)-H(D|A)= 0.17103394188

其他特征与天气特征计算信息增益方式相同，根据比较信息增益值，选择信息增益最大的值作为决策树根结点。根节点选取完成之后，根据特征项数划分子集。

特征A（天气）有三个不同的取值{sunny、overcast、rainy}，即v=3，根据特征A（天气）的取值，将数据集D划分为三个子集：
sunny的子集中有5个样本，2个打球（play=yes），3个不打球（play=no）

Overcast的子集中有4个样本，都为打球（play=yes）

Rainy的子集中有5个样本，3个打球（play=yes），2个不打球（play=no）

每个子集可以分别计算熵。
sunny熵= -(2/5)log(2/5)-(3/5)log(3/5)>0

overcast熵=-(4/4)*log(4/4)=0

rainy熵=-(3/5)log(3/5)-(2/5)log(2/5)>0

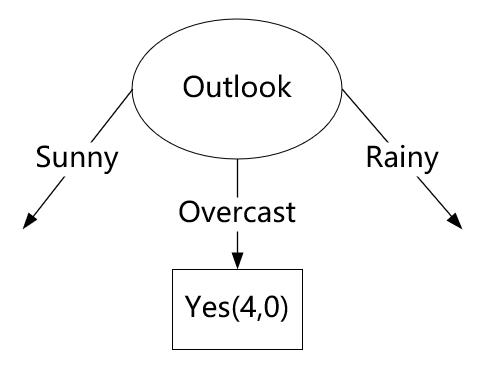
将outlook特征为sunny的子集作为划分开始构建新的决策树。

No 天气outlook temperature温度 humidity湿度 windy是否有风 play
1 sunny hot high FALSE no
2 sunny hot high TRUE no
8 sunny mild high FALSE no
9 sunny cool normal FALSE yes
11 sunny mild normal TRUE yes

得到数据集后，开始step1，同理进行计算。

最后生成决策树如下：

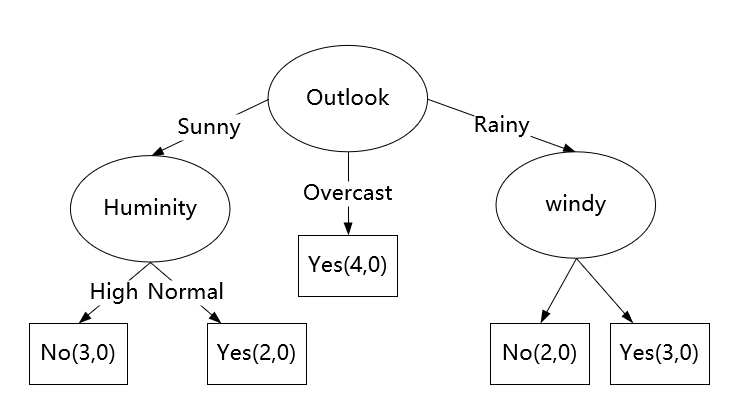
代码部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
'''计算信息熵'''
def calcEntropy(data):
    numEntities = len(data) # 样本数D
    labelCount = {} # key存放类别 value存放对应类别个数
    for line in data:
        currentLabel = line[-1]
        if currentLabel not in labelCount.keys():  #不包含此类别则加入此类别
            labelCount[currentLabel] = 0
        labelCount[currentLabel] += 1
    shannonEnt = 0.0 #信息熵
    for key in labelCount:
        prob = float(labelCount[key])/numEntities
        shannonEnt -= prob * log(prob,2)
#         print(prob)
    return shannonEnt

'''根据指定特征和特征值划分数据'''
def split_DataSet(data,axis,value):
    res_data = []
    for vec in data:
        if vec[axis]==value:
            reducedFeatVec = vec[:axis]
            reducedFeatVec.extend(vec[axis+1:])
#             print(reducedFeatVec)
            res_data.append(reducedFeatVec)
    return res_data

'''选择最优信息特征'''
def choose_best_feature(data):
    feature_size = len(data[0]) - 1
    base_entropy = calcEntropy(data)
    best_Gain = 0.0
    best_feature = -1
    for i in range(feature_size):#遍历特征
        feat_list = [temp[i] for temp in data]
#         print(feat_list)
        feat_set = set(feat_list)
        new_entropy = 0.0
        for feat_value in feat_set:
            sub_dataset = split_DataSet(data,i,feat_value)
            prob = len(sub_dataset)/float(len(data))
            new_entropy += prob * calcEntropy(sub_dataset)
        info_gain = base_entropy - new_entropy
        print(info_gain)
        if(info_gain > best_Gain):
            best_Gain = info_gain
            best_feature = i
    return best_feature

'''分类，创建字典，排序并返回出现次数最多的分类名称'''
def majority_cnt(class_list):
    class_count = {}
    for vote in class_list:
        if vote not in class_count.keys():class_count[vote] = 0
        class_count[vote] += 1
    sorted_class_count = sorted(class_count.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sorted_class_count[0][0]

'''生成决策树主方法'''
def create_tree(data,labels):
    class_list = [temp[-1] for temp in data]
    if class_list.count(class_list[0]) == len(class_list):
        return class_list[0]
    if len(class_list) == 1:
        return majority_cnt(class_list)
    best_feature = choose_best_feature(data)
    best_feat_label = labels[best_feature]
    
    mytree = {best_feat_label:{}}
    del(labels[best_feature])
    feat_values = [temp[best_feature] for temp in data]
    unique_vals = set(feat_values)
    for value in unique_vals:
        sub_label = labels[:]
        mytree[best_feat_label][value] = create_tree(split_DataSet(data,best_feature,value),sub_label)
    return mytree

def classify(input_tree,feat_labels,vec):
    firstStr = input_tree.keys()[0]
    secondDict = input_tree[firstStr]
    featIndex = feat_labels.index(firstStr)
    key = vec[featIndex]
    valueOfFeat = secondDict[key]
    if isinstance(valueOfFeat, dict): 
        classLabel = classify(valueOfFeat, featLabels, testVec)
    else: classLabel = valueOfFeat
    return classLabel

def storeTree(inputTree,filename):
    import pickle
    fw = open(filename,'w')
    pickle.dump(inputTree,fw)
    fw.close()

def grabTree(filename):
    import pickle
    fr = open(filename)
    return pickle.load(fr)

fr = open('play2.txt')
lenses =[inst.strip().split(' ') for inst in fr.readlines()]
print(lenses)
lensesLabels = ['outlook','temperature','huminidy','windy']
lensesTree =create_tree(lenses,lensesLabels)
createPlot(lensesTree)

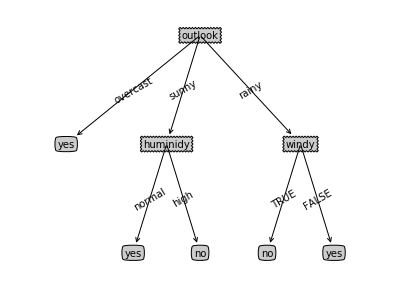
C4.5的计算和构造流程与ID3大致相同，区别在于C4.5提出了采用信息增益率（GainRate）来选择分裂特征。

其中就是ID3算法中的新增增益。

扩展

决策树还可以使用sckit-learn算法包实现。

CART:在决策树之上，二分决策树(Classification And Regression Tree)是另一种应用广泛的决策树算法。CART可以用于回归。

提升树(boostring tree):是以决策树为基本学习器的提升方法。它被认为是统计学习中性能最好的方法之一。对分类问题，提升树中的决策树是二叉决策树；对回归问题，提升树中的决策树是二叉回归树。

梯度提升树(GBT):是利用最速下降法的近似方法。其关键是利用损失函数的负梯度在当前模型的值作为残差的近似值，从而拟合一个回归树。梯度提升树用于分类模型时，是梯度提升决策树GBDT；用于回归模型时，是梯度提升回归树GBRT。

随机森林(RF)：本质是许多决策树的集合。

Xgboost：Xgboost是很多CART回归树集成，是在GBDT的基础上对boosting算法进行的改进。

lightGBM:是一个梯度 boosting 框架，使用基于学习算法的决策树。它可以说是分布式的，高效的。

参考文章链接

http://www.cnblogs.com/ooon/p/5643494.html
https://www.cnblogs.com/ooon/p/5647309.html
http://huaxiaozhuan.com/%E7%BB%9F%E8%AE%A1%E5%AD%A6%E4%B9%A0/chapters/4_decision_tree.html
http://huaxiaozhuan.com/%E7%BB%9F%E8%AE%A1%E5%AD%A6%E4%B9%A0/chapters/7_GBT.html
https://blog.csdn.net/huahuazhu/article/details/73167610?locationNum=2&fps=1
http://d0evi1.com/xgboost/
https://blog.csdn.net/github_38414650/article/details/76061893
https://blog.csdn.net/a1b2c3d4123456/article/details/52849091
https://blog.csdn.net/q383700092/article/details/60954996