之前写过如何手写ID3决策树的博客,大概讲解了一下决策树的原理和代码实现。今天这篇笔记就来详细讨论一下决策树的原理。
手写ID3决策树树的构造
决策树学习的目的是为了产生一颗泛化能力强,即处理未见示例强的决策树,基本流程遵循简单且直观的“分而治之”策略。
决策树的构造是一个递归的过程,有三种情形会导致递归返回:
(1) 当前结点包含的样本全属于同一类别,这时直接将该节点标记为叶节点,并设为相应的类别;
(2) 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分,这时将该节点标记为叶节点,并将其类别设为该节点所含样本最多的类别;
(3) 当前结点包含的样本集合为空,不能划分,这时也将该节点标记为叶节点,并将其类别设为父节点中所含样本最多的类别。
算法的基本流程如下图所示:
决策树学习的关键在于如何选择划分属性,不同的划分属性得出不同的分支结构,从而影响整颗决策树的性能。属性划分的目标是让各个划分出来的子节点尽可能地“纯”,即属于同一类别。因此下面便是介绍量化纯度的具体方法,决策树最常用的算法有三种:ID3,C4.5和CART。
划分方法
从A中选择最优划分属性,是构建决策树中最重要的一步。随着决策树划分进行,决策树的分支节点应该包含样本尽可能属于同一类别,即节点的“纯度”越来越高才对。
ID3算法
ID3算法使用信息增益为准则来选择划分属性,“信息熵”(information entropy)是度量样本结合纯度的常用指标,假定当前样本集合D中第k类样本所占比例为pk,则样本集合D的信息熵定义为:
其中Ent(D)的值越小表示D的纯度越高。易知只有一个类别时,信息熵为0。
一般来说,考虑到分支越多的样本节点影响越大,可计算出划分后相比于原始数据集D获得的“信息增益”。
ID3算法就以信息增益为准则来选择划分属性。信息增益越大,使用对应属性来划分所获得的纯度提升越大。
具体的计算样例参考之前的博客。
C4.5算法
ID3算法存在一个问题,就是偏向于取值数目较多的属性,例如:如果存在一个唯一标识,这样样本集D将会被划分为|D|个分支,每个分支只有一个样本,这样划分后的信息熵为零,十分纯净,但是对分类毫无用处。因此C4.5算法使用了“增益率”(gain ratio)来选择划分属性,来避免这个问题带来的困扰。首先使用ID3算法计算出信息增益高于平均水平的候选属性,接着C4.5计算这些候选属性的增益率,增益率定义为:
其中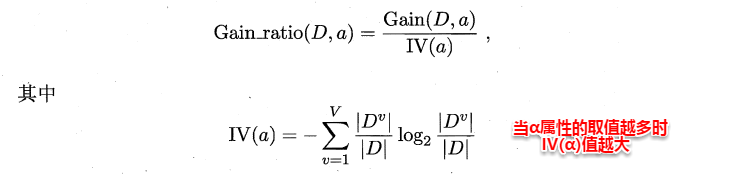
即先从候选划分属性中找出信息增益最高高于平均水平的属性,再从中选取最高的。
CART
CART采用基尼指数来选择划分属性。基尼指数反映的是从样本集D中随机抽取两个样本,其类别标记不一致的概率,因此Gini(D)越小越好。数据集D的纯度用基尼值衡量:
使用属性α划分后的基尼指数为: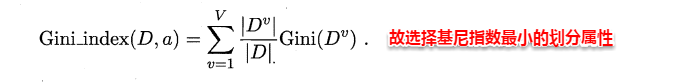
剪枝
剪枝是决策树中处理过拟合的主要手段。决策树学习过程中,结点划分不断重复,有时会造成决策树分支过多,进而导致过拟合。因此,需要通过一些手段主动的去掉一些分支。
主要有两种手段,预剪枝和后剪枝。
- 预剪枝(prepruning):在构造的过程中先评估,再考虑是否分支。
- 后剪枝(post-pruning):在构造好一颗完整的决策树后,自底向上,评估分支的必要性。
预剪枝
预剪枝处理使得决策树的很多分支被剪掉,因此大大降低了训练时间开销,同时降低了过拟合的风险,但另一方面由于剪枝同时剪掉了当前节点后续子节点的分支,因此预剪枝“贪心”的本质阻止了分支的展开,在一定程度上带来了欠拟合的风险。
后剪枝
后剪枝则通常保留了更多的分支,因此采用后剪枝策略的决策树性能往往优于预剪枝,但其自底向上遍历了所有节点,并计算性能,训练时间开销相比预剪枝大大提升。
连续值和缺失值处理
连续值
对于连续值的属性,若每个取值作为一个分支则显得不可行,因此需要进行离散化处理,常用的方法为二分法,基本思想为:给定样本集D与连续属性α,二分法试图找到一个划分点t将样本集D在属性α上分为≤t与>t。
- 首先将α的所有取值按升序排列,所有相邻属性的均值作为候选划分点(n-1个,n为α所有的取值数目)。
- 计算每一个划分点划分集合D(即划分为两个分支)后的信息增益。
- 选择最大信息增益的划分点作为最优划分点。
缺失值
现实中常会遇到不完整的样本,即某些属性值缺失。有时若简单采取剔除,则会造成大量的信息浪费,因此在属性值缺失的情况下需要解决两个问题:(1)如何选择划分属性。(2)给定划分属性,若某样本在该属性上缺失值,如何划分到具体的分支上。
总结
很早之前已经看过决策树,当时跟着博客实现了ID3算法。现在又看了一遍理论,印象应该更深了一点。这次重点看了剪枝问题,以及连续值和缺失值问题。未完善的地方后面再补充。